Volume 17, Issue 1 (March 2019)
Iranian Rehabilitation Journal 2019, 17(1): 49-52 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Rastegar M, Bakhshi E, Hosseinzadeh S. Binary Regression With a Misclassified Response Variable in Diabetes Data. Iranian Rehabilitation Journal 2019; 17 (1) :49-52
URL: http://irj.uswr.ac.ir/article-1-779-en.html
URL: http://irj.uswr.ac.ir/article-1-779-en.html
1- Department of Biostatistics, University of Social Welfare and Rehabilitation Sciences, Tehran, Iran.
Full-Text [PDF 483 kb]
(1622 Downloads)
| Abstract (HTML) (4308 Views)
Full-Text: (990 Views)
1. Introduction
Outcome misclassification is prevalent in epidemiology and has important impacts on parameter estimates and statistical inference. The issue of misclassification in 2×2 tables has first been considered by Bross [1-4] and a review study was conducted by Chen on this subject [5].
Neuhaus analyzed the bias size of misclassification error correction in the response variable and reported except for when the sensitivity and specificity are both large, ignoring the misclassification correction leads to a biased estimate of the effect of exposures [6]. Researchers often use logistic regression to estimate the effect of exposures on the binary response variable. Tang et al. used logistic regression to correct misclassification in estimating the coefficients and the maximum likelihood estimation [7].
Davidov et al. used logistic regression to correct the coefficients of the models with misclassification error [8]. In medicine and epidemiology, the classification issue is of particular importance with respect to the stage of the disease or the condition of exposure to the risk factor. In these studies, after classifying the subjects, based on the status of exposure and infection, the data are classified to create some statistical indicators (e.g. odds ratio and relative risk) for measuring the relationship between the predictor variables and the response variable [9].
This cross-sectional study with a misclassified binary outcome used a method proposed by Lyles et al. [10]. We applied the maximum likelihood method to identify and correct misclassification in binary variables [6].
2. Methods
Data from the Diabetes Screening test in the Health Center of Zahedan City, Iran, were investigated in this cross-sectional study. It included 819 Iranian adults with the binary response variable of Type 2 Diabetes Mellitus (T2DM). The main purpose of the analysis was to model the association between T2DM and hypertension, obesity, and age. However, in practice, T2DM may be diagnosed by error-prone test and the misclassification in diagnoses compromises the adjusted OR estimation and statistical inference.
Using a method proposed by Lyles et al. [10], we examined the relationship between age, hypertension, obesity, and T2DM in 819 Iranian adults. Statistical analysis was performed using SAS and P<0.05 were considered as statistically significant. T2DM was defined as a binary outcome variable. Age: Information about the respondent’s age was obtained based on their self-reported birth year and was considered as a continuous covariate. Hypertension: The study participants were diagnosed with hypertension if their systolic blood pressure was ˃140 mmHg, or if their diastolic blood pressure was ˃90 mmHg. Obesity: Individuals with a Body Mass Index (BMI) ≥30 kg/m2 were considered obese and <30 kg/m2 as non-obese.
3. Results
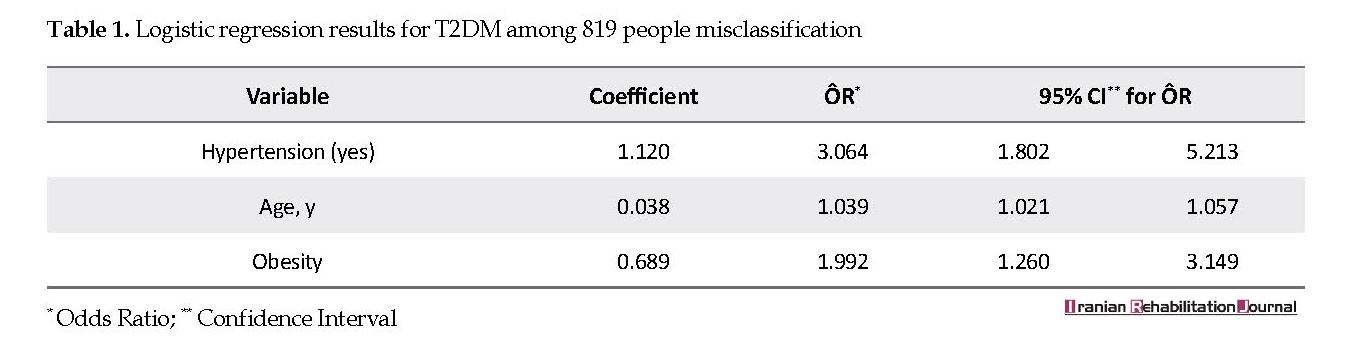
The Mean±SD age of subjects was 47.65±12.23 years. Of participants, 462(56%) were men and 190(23.2%) were obese. Among participants, 15.8% and 15.5% were diabetic and had high hypertension, respectively. Logistic regression model was used in the new model. The regression coefficients and odds ratios are presented in Table 1. The odds ratio of people with hypertension equaled to 3.06 (95% CI=1.80-5.21), compared with those without hypertension. The estimated ÔR for age is 1.04 (95% CI=1.02-1.06).This means that increased age enhances the odds of T2DM occurrence. The estimated ÔR for obese people is 1.992 (95% CI=1.260-3.149), compared with non-obese ones.
4. Discussion
Specific motivation for these developments is provided by cross-sectional data on the assessments of T2DM and hypertension status and covariates measured in the Diabetes Screening test. We specified likelihood functions corresponding to main/internal validation study designs to solve the problem of outcome misclassification in logistic regression [11, 12]. Thus, we incorporated validation data and covariates into misclassification models. Although validation data based on maximum likelihood methods are outlined in the comprehensive text of Carroll et al. [13], a study generalized the logistic regression-based approach [7] which only outcome misclassification was addressed. It also makes AIC calculations available and the AIC indicator was used to select the appropriate model [14]. Consistent with some studies, our results revealed a positive association between age and T2DM.
Outcome misclassification is prevalent in epidemiology and has important impacts on parameter estimates and statistical inference. The issue of misclassification in 2×2 tables has first been considered by Bross [1-4] and a review study was conducted by Chen on this subject [5].
Neuhaus analyzed the bias size of misclassification error correction in the response variable and reported except for when the sensitivity and specificity are both large, ignoring the misclassification correction leads to a biased estimate of the effect of exposures [6]. Researchers often use logistic regression to estimate the effect of exposures on the binary response variable. Tang et al. used logistic regression to correct misclassification in estimating the coefficients and the maximum likelihood estimation [7].
Davidov et al. used logistic regression to correct the coefficients of the models with misclassification error [8]. In medicine and epidemiology, the classification issue is of particular importance with respect to the stage of the disease or the condition of exposure to the risk factor. In these studies, after classifying the subjects, based on the status of exposure and infection, the data are classified to create some statistical indicators (e.g. odds ratio and relative risk) for measuring the relationship between the predictor variables and the response variable [9].
This cross-sectional study with a misclassified binary outcome used a method proposed by Lyles et al. [10]. We applied the maximum likelihood method to identify and correct misclassification in binary variables [6].
2. Methods
Data from the Diabetes Screening test in the Health Center of Zahedan City, Iran, were investigated in this cross-sectional study. It included 819 Iranian adults with the binary response variable of Type 2 Diabetes Mellitus (T2DM). The main purpose of the analysis was to model the association between T2DM and hypertension, obesity, and age. However, in practice, T2DM may be diagnosed by error-prone test and the misclassification in diagnoses compromises the adjusted OR estimation and statistical inference.
Using a method proposed by Lyles et al. [10], we examined the relationship between age, hypertension, obesity, and T2DM in 819 Iranian adults. Statistical analysis was performed using SAS and P<0.05 were considered as statistically significant. T2DM was defined as a binary outcome variable. Age: Information about the respondent’s age was obtained based on their self-reported birth year and was considered as a continuous covariate. Hypertension: The study participants were diagnosed with hypertension if their systolic blood pressure was ˃140 mmHg, or if their diastolic blood pressure was ˃90 mmHg. Obesity: Individuals with a Body Mass Index (BMI) ≥30 kg/m2 were considered obese and <30 kg/m2 as non-obese.
3. Results
The Mean±SD age of subjects was 47.65±12.23 years. Of participants, 462(56%) were men and 190(23.2%) were obese. Among participants, 15.8% and 15.5% were diabetic and had high hypertension, respectively. Logistic regression model was used in the new model. The regression coefficients and odds ratios are presented in Table 1. The odds ratio of people with hypertension equaled to 3.06 (95% CI=1.80-5.21), compared with those without hypertension. The estimated ÔR for age is 1.04 (95% CI=1.02-1.06).This means that increased age enhances the odds of T2DM occurrence. The estimated ÔR for obese people is 1.992 (95% CI=1.260-3.149), compared with non-obese ones.
4. Discussion
Specific motivation for these developments is provided by cross-sectional data on the assessments of T2DM and hypertension status and covariates measured in the Diabetes Screening test. We specified likelihood functions corresponding to main/internal validation study designs to solve the problem of outcome misclassification in logistic regression [11, 12]. Thus, we incorporated validation data and covariates into misclassification models. Although validation data based on maximum likelihood methods are outlined in the comprehensive text of Carroll et al. [13], a study generalized the logistic regression-based approach [7] which only outcome misclassification was addressed. It also makes AIC calculations available and the AIC indicator was used to select the appropriate model [14]. Consistent with some studies, our results revealed a positive association between age and T2DM.
Age is generally a critical factor of developing diabetes [15, 16]. In line with some studies, we also found that T2DM was almost 3 times as likely to develop in subjects with hypertension as in subjects with normal blood pressure. Other concerning factors may exist; e.g. reducing blood pressure decreases albuminuria in T2DM. In a randomized controlled trial, the management of blood pressure was considered a high priority in the treatment of T2DM [17]. Consistent with some studies, our results supported that obesity plays a major role in T2DM [15]. Increasing physical activity and improving nutritional diet can reduce obesity and T2DM.
We failed to establish a causal association between factors and T2DM, or specify the direction of such association. Although we adjusted our analyses for confounders, our model has not included other factors associated with T2DM, such as longer diabetes duration, family history, and ethnicity.
5. Conclusion
The method provided adjusting for biases due to misclassification in binary response in logistic regression, and using it is recommended. Logistic regression methods with misclassified data are appropriate choices to estimate the correct odds ratio in potential misclassified response variable. Using logistic regression for misclassified data validation suggested that blood pressure has a significant effect on diabetes. It is suggested that the logistic regression method be used to correct the odds ratio in terms of the probability of misclassification error in the screening data.
Ethical Considerations
Compliance with ethical guidelines
The study was approved by the Research Ethics Committee of the University of Social Welfare and Rehabilitation Sciences (IR.USWR.REC.1397.30).
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Authors contributions
Conceptualization and methodology: Enayatollah Bakhshi; Investigation: Maryam Rastegar; Writing original draft: Maryam rastegar and Sammaneh Hoseinzadeh; and Writing review & editing: All authors.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
The authors thank Zahedan health center staff who helped to collect the data.
References
Bross I. Misclassification in 2×2 tables. Biometrics. 1954; 10(4):478-86. [DOI:10.2307/3001619]
Newell DJ. Errors in the interpretation of errors in epidemiology. American Journal of Public Health and the Nations Health. 1962; 52(11):1925-8. [DOI:10.2105/AJPH.52.11.1925] [PMCID]
Koch GG. The effect of non-sampling errors on measures of association in 2×2 contingency tables. Journal of the American Statistical Association. 1969; 64(327):852-63. [DOI:10.1080/01621459.1969.10501017]
Goldberg JD. The effects of misclassification on the bias in the difference between two proportions and the relative odds in the fourfold table. Journal of the American Statistical Association. 1975; 70(351a):561-7. [DOI:10.1080/01621459.1975.10482472]
Chen TT. A review of methods for misclassified categorical data in epidemiology. Statistics in Medicine. 1989; 8(9):1095-106. [DOI:10.1002/sim.4780080908] [PMID]
Neuhaus JM. Bias and efficiency loss due to misclassified responses in binary regression. Biometrika. 1999; 86(4):843-55. [DOI:10.1093/biomet/86.4.843]
Tang L, Lyles RH, King CC, Celentano DD, Lo Y. Binary regression with differentially misclassified response and exposure variables. Statistics in Medicine. 2015; 34(9):1605-20. [DOI:10.1002/sim.6440] [PMID] [PMCID]
Davidov O, Faraggi D, Reiser B. Misclassification in logistic regression with discrete covariates. Biometrical Journal: Journal of Mathematical Methods in Biosciences. 2003; 45(5):541-53. [DOI:10.1002/bimj.200390031]
Duffy SW, Warwick J, Williams AR, Keshavarz H, Kaffashian F, Rohan TE, et al. A simple model for potential use with a misclassified binary outcome in epidemiology. Journal of Epidemiology & Community Health. 2004; 58(8):712-7. [DOI:10.1136/jech.2003.010546] [PMID] [PMCID]
Lyles RH, Tang L, Superak HM, King CC, Celentano DD, Lo Y, et al. Validation data-based adjustments for outcome misclassification in logistic regression: An illustration. Epidemiology. 2011; 22(4):589-97. [DOI:10.1097/EDE.0b013e3182117c85] [PMID] [PMCID]
Tang L, Lyles RH, Ye Y, Lo Y, King CC. Extended matrix and inverse matrix methods utilizing internal validation data when both disease and exposure status are misclassified. Epidemiologic Methods. 2013; 2(1):49-66. [DOI:10.1515/em-2013-0008] [PMID] [PMCID]
Barron BA. The effects of misclassification on the estimation of relative risk. Biometrics. 1977; 33(2):414-8. [DOI:10.2307/2529795] [PMID]
Carroll RJ, Ruppert D, Crainiceanu CM, Stefanski LA. Measurement error in nonlinear models: A modern perspective. Boca Raton, Florida: Chapman and Hall/CRC; 2006. [DOI:10.1201/9781420010138]
Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974; 19(6):716-23. [DOI:10.1109/TAC.1974.1100705]
Yang A, Kim J, Cho SY, Jin DK. Prevalence and risk factors for type 2 diabetes mellitus with Prader–Willi syndrome: A single center experience. Orphanet Journal of Rare Diseases. 2017; 12:146. [DOI:10.1186/s13023-017-0702-5] [PMID] [PMCID]
Liu Y, Yang J, Tao L, Lv H, Jiang X, Zhang M, et al. Risk factors of diabetic retinopathy and sight-threatening diabetic retinopathy: A cross-sectional study of 13 473 patients with type 2 diabetes mellitus in mainland China. BMJ Open. 2017; 7(9):e016280. [DOI:10.1136/bmjopen-2017-016280] [PMID] [PMCID]
UK Prospective Diabetes Study Group. Tight blood pressure control and risk of macrovascular and microvascular complications in type 2 diabetes: UKPDS 38. BMJ. 1998; 317(7160):703-13. [DOI:10.1136/bmj.317.7160.703] [PMID] [PMCID]
We failed to establish a causal association between factors and T2DM, or specify the direction of such association. Although we adjusted our analyses for confounders, our model has not included other factors associated with T2DM, such as longer diabetes duration, family history, and ethnicity.
5. Conclusion
The method provided adjusting for biases due to misclassification in binary response in logistic regression, and using it is recommended. Logistic regression methods with misclassified data are appropriate choices to estimate the correct odds ratio in potential misclassified response variable. Using logistic regression for misclassified data validation suggested that blood pressure has a significant effect on diabetes. It is suggested that the logistic regression method be used to correct the odds ratio in terms of the probability of misclassification error in the screening data.
Ethical Considerations
Compliance with ethical guidelines
The study was approved by the Research Ethics Committee of the University of Social Welfare and Rehabilitation Sciences (IR.USWR.REC.1397.30).
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Authors contributions
Conceptualization and methodology: Enayatollah Bakhshi; Investigation: Maryam Rastegar; Writing original draft: Maryam rastegar and Sammaneh Hoseinzadeh; and Writing review & editing: All authors.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
The authors thank Zahedan health center staff who helped to collect the data.
References
Bross I. Misclassification in 2×2 tables. Biometrics. 1954; 10(4):478-86. [DOI:10.2307/3001619]
Newell DJ. Errors in the interpretation of errors in epidemiology. American Journal of Public Health and the Nations Health. 1962; 52(11):1925-8. [DOI:10.2105/AJPH.52.11.1925] [PMCID]
Koch GG. The effect of non-sampling errors on measures of association in 2×2 contingency tables. Journal of the American Statistical Association. 1969; 64(327):852-63. [DOI:10.1080/01621459.1969.10501017]
Goldberg JD. The effects of misclassification on the bias in the difference between two proportions and the relative odds in the fourfold table. Journal of the American Statistical Association. 1975; 70(351a):561-7. [DOI:10.1080/01621459.1975.10482472]
Chen TT. A review of methods for misclassified categorical data in epidemiology. Statistics in Medicine. 1989; 8(9):1095-106. [DOI:10.1002/sim.4780080908] [PMID]
Neuhaus JM. Bias and efficiency loss due to misclassified responses in binary regression. Biometrika. 1999; 86(4):843-55. [DOI:10.1093/biomet/86.4.843]
Tang L, Lyles RH, King CC, Celentano DD, Lo Y. Binary regression with differentially misclassified response and exposure variables. Statistics in Medicine. 2015; 34(9):1605-20. [DOI:10.1002/sim.6440] [PMID] [PMCID]
Davidov O, Faraggi D, Reiser B. Misclassification in logistic regression with discrete covariates. Biometrical Journal: Journal of Mathematical Methods in Biosciences. 2003; 45(5):541-53. [DOI:10.1002/bimj.200390031]
Duffy SW, Warwick J, Williams AR, Keshavarz H, Kaffashian F, Rohan TE, et al. A simple model for potential use with a misclassified binary outcome in epidemiology. Journal of Epidemiology & Community Health. 2004; 58(8):712-7. [DOI:10.1136/jech.2003.010546] [PMID] [PMCID]
Lyles RH, Tang L, Superak HM, King CC, Celentano DD, Lo Y, et al. Validation data-based adjustments for outcome misclassification in logistic regression: An illustration. Epidemiology. 2011; 22(4):589-97. [DOI:10.1097/EDE.0b013e3182117c85] [PMID] [PMCID]
Tang L, Lyles RH, Ye Y, Lo Y, King CC. Extended matrix and inverse matrix methods utilizing internal validation data when both disease and exposure status are misclassified. Epidemiologic Methods. 2013; 2(1):49-66. [DOI:10.1515/em-2013-0008] [PMID] [PMCID]
Barron BA. The effects of misclassification on the estimation of relative risk. Biometrics. 1977; 33(2):414-8. [DOI:10.2307/2529795] [PMID]
Carroll RJ, Ruppert D, Crainiceanu CM, Stefanski LA. Measurement error in nonlinear models: A modern perspective. Boca Raton, Florida: Chapman and Hall/CRC; 2006. [DOI:10.1201/9781420010138]
Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974; 19(6):716-23. [DOI:10.1109/TAC.1974.1100705]
Yang A, Kim J, Cho SY, Jin DK. Prevalence and risk factors for type 2 diabetes mellitus with Prader–Willi syndrome: A single center experience. Orphanet Journal of Rare Diseases. 2017; 12:146. [DOI:10.1186/s13023-017-0702-5] [PMID] [PMCID]
Liu Y, Yang J, Tao L, Lv H, Jiang X, Zhang M, et al. Risk factors of diabetic retinopathy and sight-threatening diabetic retinopathy: A cross-sectional study of 13 473 patients with type 2 diabetes mellitus in mainland China. BMJ Open. 2017; 7(9):e016280. [DOI:10.1136/bmjopen-2017-016280] [PMID] [PMCID]
UK Prospective Diabetes Study Group. Tight blood pressure control and risk of macrovascular and microvascular complications in type 2 diabetes: UKPDS 38. BMJ. 1998; 317(7160):703-13. [DOI:10.1136/bmj.317.7160.703] [PMID] [PMCID]
Article type: Original Research Articles |
Subject:
Biostatistics
Received: 2018/09/14 | Accepted: 2019/01/5 | Published: 2019/03/1
Received: 2018/09/14 | Accepted: 2019/01/5 | Published: 2019/03/1
Send email to the article author